Tweet

Contents | 1. Introduction to structural design | 2. Loads | 3. Wood | 4. Steel | 5. Reinforced concrete

Introduction to steel | Material properties | Sectional properties | Design approaches | Construction systems | Tension elements | Columns | Beams | Connections | Ch. 4 Appendix

Chapter 4 — Steel: Beams

The design of steel wide-flange beams using the "allowable strength design" method is quite similar to the procedures used to design timber beams (see Chapter 3). Cross sections are selected based on their strength in bending, and then checked for shear and deflection.

Bending of laterally-braced and compact beams

Unlike wood beams, however, steel beams are designed based on their "available" strength, rather than on the more convention notion of an "allowable" stress. Whereas the strength of a wood beam corresponds to its outer fibers reaching a failure stress, steel beams do not fail when their outer fibers first begin to yield at the stress, F_y. A steel cross section is able to carry increased loads beyond the so-called elastic moment, shown in Figure 4.21a, up until the entire cross section has yielded, as shown in Figure 4.21b. The plastic section modulus corresponds to this so-called plastic moment, reached when the strain at a cross section is of sufficient magnitude so that virtually the entire section has yielded.

Figure 4.21: Bending stresses acting on steel wide-flange (-shaped) cross section corresponding to the (a) elastic moment and (b) plastic moment, with three examples: (c) and (d) illustrate elastic and plastic moments for a hypothetical section with all its area at the extreme fibers; (e) and (f) illustrate elastic and plastic moments for a typical W30 × 90 section; while (g) and (h) illustrate elastic and plastic moments for a rectangular section.

Previously, steel used an "allowable stress" method based on a limit state corresponding to the elastic moment; and if the plastic moment were always stronger than the elastic moment to the same extent for all cross sections, one could simply adjust the factor of safety for allowable strength (plastic moment) design so that the method corresponded precisely to allowable stress (elastic moment) design. However, it can be shown that the extra margin of safety gained by moving beyond the elastic, to the plastic moment (i.e., from the condition of Figure 4.21a to Figure 4.21b), is not the same for all cross sections, so that allowable stress design for steel does not provide a consistent margin of safety against the limit state of complete yielding.

For wide-flange (-shaped) sections, the extremes can be represented by a hypothetical section with no web (i.e., consisting entirely of flanges of infinite density, or no thickness, as shown in Figures 4.21c and 4.21d); and, at the other extreme, a section whose flanges merge together at the neutral axis (i.e., a rectangular section, as shown in Figures 4.21g and 4.21h). In the first case, it is clear that the elastic moment and plastic moment coincide, and the so-called "shape factor" defining the ratio of plastic to elastic section modulus, Z_x/S_x, equals 1.0. In the second case, the elastic section modulus can be computed by examining the rotational equilibrium of the force resultants shown in Figure 4.21g. Since the moment arm between them equals (2/3)h, and the resultant force, C, equals (1/2)(h/2)(b)(F_y), the moment, M, equals (2/3)(h)(1/2)(h/2)(b)(F_y ) and, solving for the section modulus, S_x = M/F_y, we get S_x = bh²/6. Performing the same equilibrium calculation on Figure 4.21h (with a moment arm equal to h/2), and solving for the plastic section modulus, Z_x = M/F_y , we get Z_x = bh²/4. The shape factor in this case is Z_x/S_x = 1.5.

Clearly, all -shaped sections must have a shape factor between these two extremes, i.e., between 1.0 and 1.5. The shape factor for a typical W-shape (W30 × 90), shown in Figures 4.21e and 4.21f, can be determined in the same manner, abstracting from the complexities of the actual shape by considering only perfectly rectangular flange and web areas. Using the dimensions shown, and performing the same equilibrium calculations as in the cases above, we get S_x = 240 in³ and Z_x = 277 in³, so the shape factor, Z_x/S_x = 277/240 = 1.15. The actual values for elastic and plastic section modulus are found in Appendix Table A-4.3, and it can be seen that the approximate calculations are both conservative and reasonably accurate: the correct values are actually S_x = 245 in³ and Z_x = 283 in³, so the real shape factor, Z_x/S_x = 283/245 = 1.16.

The equation for plastic section modulus, Z_x = M/F_y, presumes that the cross section is able to reach a state of complete yielding before one of two types of buckling occurs: either lateral-torsional buckling within any unbraced segment along the length of the span or local flange or web buckling. Therefore, to use this equation in design, based on the maximum moment encountered, the beam must be protected from both of these buckling modes, in the first case by limiting the effective length and, in the second case, by regulating the proportions of the beam flange and web (i.e., using a so-called compact section). Then, rewriting this equation in the form most useful for steel design, we get:

where M_max = the maximum bending moment (in-kips), F_y is the yield stress of the steel (ksi), and Ω is a safety factor equal to 1.67 for bending. The units of the required plastic section modulus are in³.

We found earlier that the shape factor for a W30 × 90 section equals 1.16. By looking at the ratio of plastic to elastic section modulus for all wide-flange shapes, it can be seen that these shape factors fall between 1.098 (for a W14 × 90), and 1.297 (for a W14 × 730). One could therefore conservatively create a safety factor for elastic allowable stress design by assuming a shape factor of 1.10, and by multiplying this value by the safety factor for allowable strength design, 1/Ω = 1/1.67 = 0.60 (inverted to be consistent with the conventions for allowable stress safety factors). Equation 4.12 would then become S_req = M_max /(1.1 × 0.6 × F_y ) = M_max / (0.66F_y). This, in fact, is the design equation for what used to be called "allowable stress design" in steel. It may still be used, but will give slightly conservative values compared with the available stress method using the plastic section modulus, Z_x. Choosing the lightest (i.e., most economical) laterally-braced, compact section is facilitated by the use of tables in which steel cross sections are ranked, first in terms of plastic section modulus, and then by least weight. Appendix Table A-4.15 is an example of such a list, in which only the lightest sections appear. Thus, a W30 × 191 (with a plastic section modulus of 675 in³) is not listed, since a lighter section, W40 × 167, has a higher plastic section modulus (693 in³).

Bending of laterally-unsupported or noncompact beams

When the compression flange of a beam is not continuously braced, lateral-torsional buckling can reduce the available bending moment below the value of M_p/Ω assumed earlier for laterally braced beams. How much this stress is reduced depends on whether the beam buckles before or after the cross section begins to yield, and how bending stresses vary over the beam's effective length. Figure 4.22 shows several possible stress stages for a cross-sectional shape as the bending moment increases. At Figure 4.22c, the outer fibers begin to yield, and the elastic moment, M_y, is reached. At Figure 4.22d and Figure 4.22e, yielding progresses further into the cross section, as the moment increases. Finally, at Figure 4.22f, the entire cross section has yielded at the maximum plastic moment that the section can sustain.

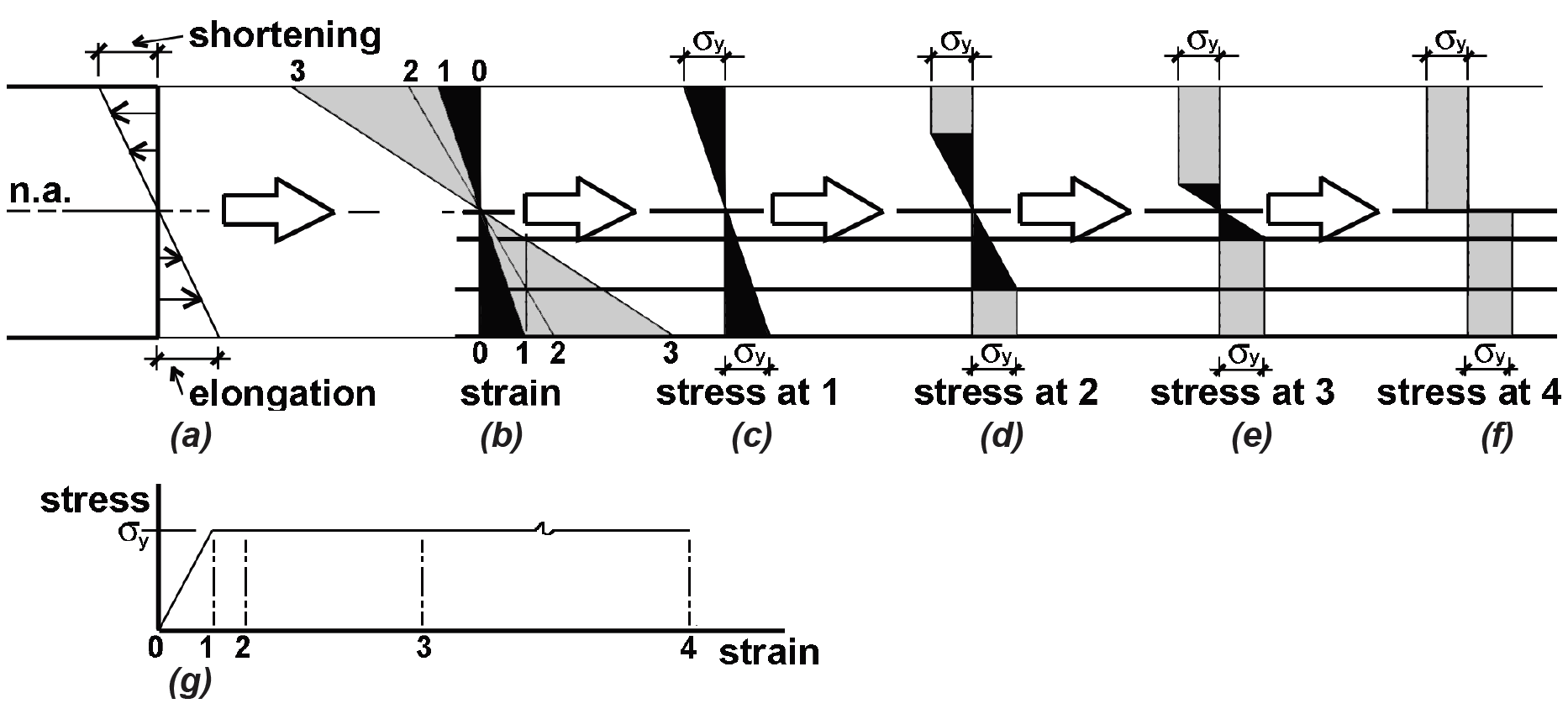
Being able to resist the full plastic moment represents an extra margin of safety: if a beam can develop this plastic moment without buckling, the maximum available bending moment of M_p/Ω is used, as shown in Equation 4.12. In addition to lateral-torsional buckling (Figure 4.23a), various types of local flange and web buckling must also be prevented from occurring before the plastic moment is reached (Figure 4.23b). Local buckling is prevented by limiting the ratio of flange width to flange thickness, as well as web width to web thickness. Sections proportioned so that local buckling will not occur are called compact sections; these sections must be used to qualify for the full available moment of M_p/Ω. As it turns out, all but one of the wide-flange shapes listed in Appendix Table A-4.3 are compact sections when made from A36 steel (the exception being W6 × 15). For 50 ksi steel, all but ten (W6 × 8.5, W6 × 9, W6 × 15, W8 × 10, W8 × 31, W10 × 12, W12 × 65, W14 × 90, W14 × 99, and W21 × 48) are compact.

Figure 4.23: Two modes of buckling limiting the strength of a wide-flange (-shaped) beam: (a) lateral-torsional buckling; and (b) local flange buckling

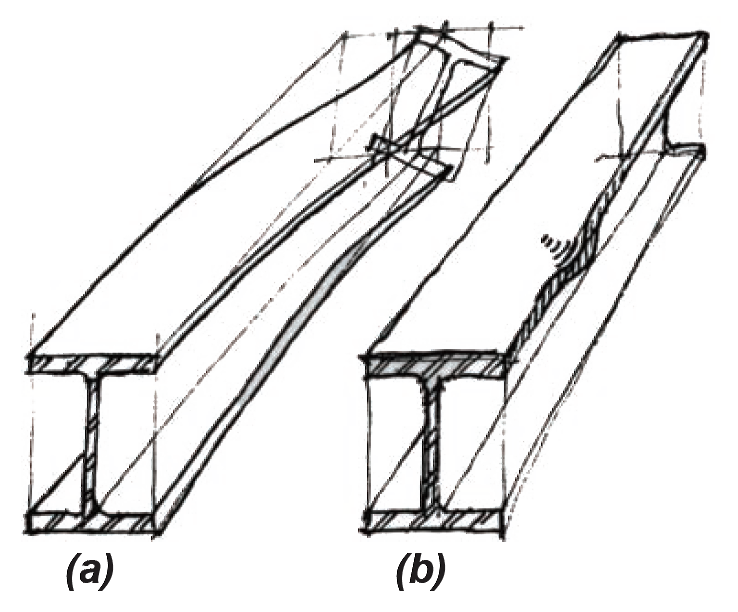
For sections that are compact and laterally braced, Equation 4.12 applies, and the full strength of the beam is utilized. However, as shown in Figure 4.24, this available strength must be reduced if either local flange buckling (where the section is not compact) or lateral-torsional buckling (where the section is not adequately braced) occurs before the plastic moment is reached.

Lateral-torsional buckling

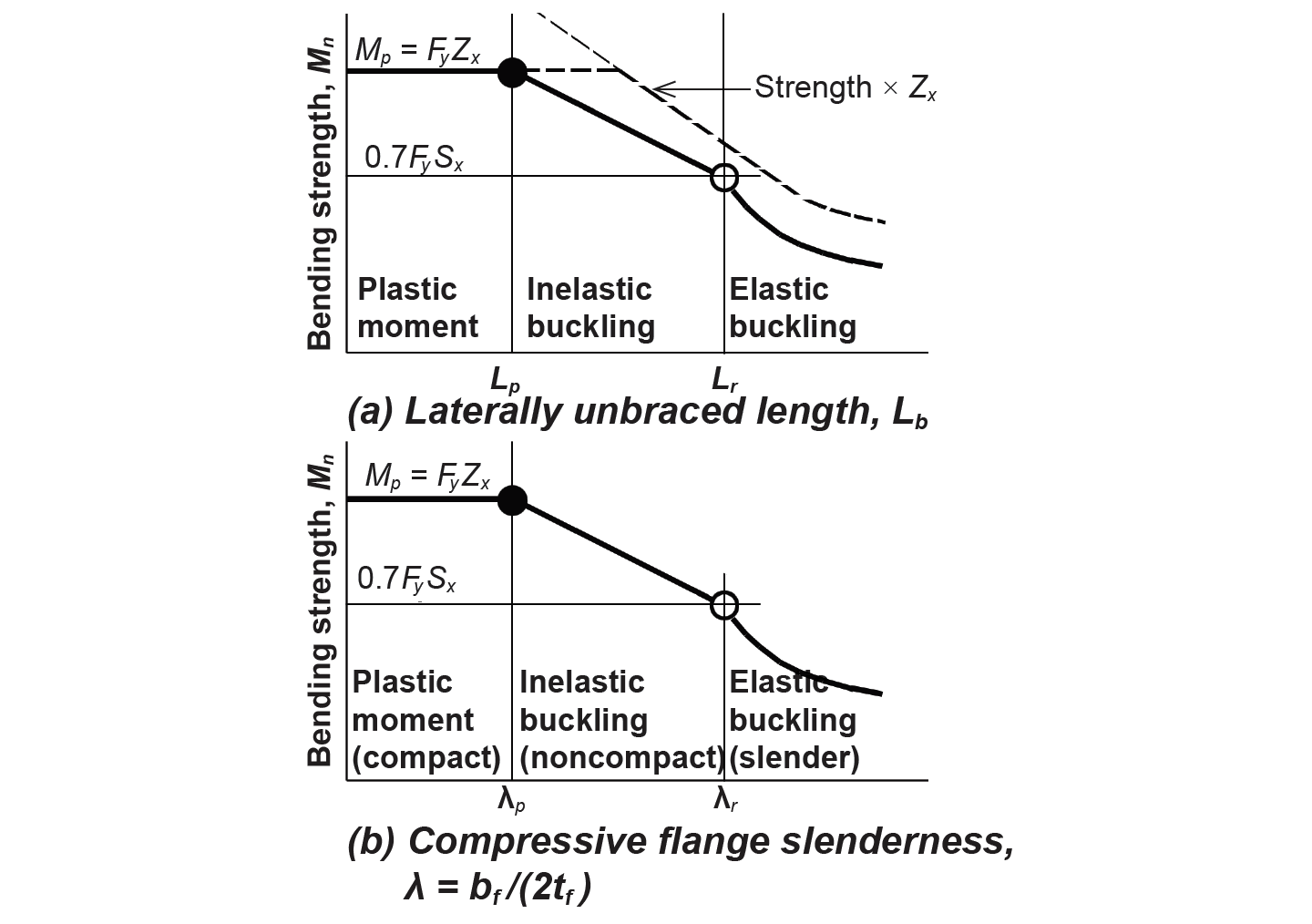
For beams with an unbraced length, L_b, that falls within the "middle zone" illustrated in Figure 4.24a (i.e., where the onset of buckling occurs before a full plastic moment, but after the elastic moment, is reached), the nominal bending strength is linearly reduced from the full plastic moment, M_p = F_yZ_x, to 70% of the elastic moment, or 0.7F_yS_x. The two boundaries (unbraced lengths) that bracket this condition of inelastic lateral-torsional buckling are called L_p and L_r. For an unbraced length, L_b, less than L_p, lateral-torsional buckling is not an issue, as the full plastic moment can be reached. For an unbraced length greater than L_r, the onset of lateral-torsional buckling is characterized entirely by elastic behavior, and the nominal bending strength must be reduced even further. These boundaries are defined as follows: L_p is set at 1.76r_y, where E is the modulus of elasticity (29,000 ksi for all steel), F_y is the yield stress (50 ksi for A992 steel, and 36 ksi for A36 steel), and r_y is the minimum radius of gyration about the y-axis (see Appendix Table A-4.3 for wide-flange shapes). The other boundary, L_r, can be conservatively approximated as πr_ts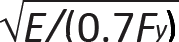, where r_ts may itself be approximated as the radius of gyration for the compression flange and part of the web; i.e., r_ts = b_f/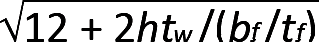. In this equation, b_f and t_f are the flange width and thickness, respectively, and h is the length of the "straight" part of the web (i.e., the clear distance between flanges, minus the radii at the web-flange intersections).

However, all these equations are based on the assumption that the beam is subject to a uniform bending moment along its entire length; where the moment varies, as is almost always the case, this assumption is overly conservative, since lateral-torsional buckling is less likely to be triggered where bending stresses are not entirely at their maximum value along the whole length of an unbraced segment. For this reason, a coefficient, C_b, should be applied to the available strength of each unbraced segment of the beam, based on the distribution and magnitude of bending moments along that segment's length. This "lateral-torsional buckling modifier" is defined as follows for doubly-symmetric bending elements such as wide-flange beams:

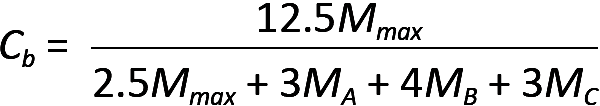
where M_max is the greatest moment within the unbraced segment; and M_A, M_B, and M_C are the bending moments at the quarter point, midpoint, and three-quarters point, respectively, along the segment. Where a segment is not braced at its endpoint (for example, where the end of a cantilevered beam is not braced), C_b should be taken as 1.0. Of course, C_b is not used where a beam is laterally braced and, in any case, can never increase the nominal bending strength beyond the plastic moment, M_p, as shown in Figure 4.24a.

Local flange buckling

Compact sections are proportioned so that neither the flange nor the web will buckle locally before the onset of a plastic moment. Since all wide-flange webs meet the standards for compact sections, only the flange slenderness, defined as λ = b_f/(2t_f ), is at issue (where b_f and t_f are the flange width and thickness, respectively). In much the same way that boundaries are established for unbraced length that define the reduction in the bending strength due to lateral-torsional buckling (Figure 4.24a), similar boundaries are established for flange slenderness, with similar consequences for beam strength (Figure 4.24b). The limit for compact behavior — i.e., the maximum flange slenderness for which beams are still able to reach the plastic moment without local flange buckling — is defined by λ_p = 0.38. The other boundary (i.e., the maximum flange slenderness for which inelastic behavior characterizes the onset of local flange buckling) is defined by λ_r = 1.0. In these equations, E is the modulus of elasticity of steel (29,000 ksi) and F_y is the material's yield stress (50 ksi for A992 steel, and 36 ksi for A36 steel). As with reductions for lateral-torsional buckling, the nominal bending strength begins with the plastic moment, M_p = F_yZ_x, for compact sections, and is linearly reduced to 70% of the elastic moment, or 0.7F_yS_x, between λ_p and λ_r, with further reductions beyond λ_r.

Where a beam is both noncompact and laterally unbraced, both criteria illustrated in Figure 4.24 are tested, and the smaller capacity governs. For beams that are both compact and laterally braced, Appendix Table A-4.15 can be used to select the lightest W-shape for bending. For A992 wide-flange beams that are not adequately braced laterally (i.e, where L_b > L_p), Appendix Table A-4.16 can be used to select the lightest beam. Of course, by setting the unbraced length to zero, Appendix Table A-4.16 can be used for laterally-braced beams as well.

Shear

Once a selection is made based on bending stress, the section is then checked for shear and deflection. The nominal shear strength, V_n , equals 0.6F_yA_w, where F_y is the yield stress of the steel and A_w is the web area (equal to the beam depth times the web thickness, d × t_w). For most cross sections, the safety factor can be taken as Ω = 1.5, so that the available strength is V_n/Ω = 0.6/Ω(F_yA_w) = 0.4F_yA_w. This can be converted into an "allowable stress" equation by defining the allowable shear stress, F_v = 0.4F_y, and solving for the required web area for a given shear force, V:

For a small group of wide-flange beams with slender webs, the safety factor for shear is increased from 1.5 to 1.67, and so the allowable shear stress becomes F_v = (0.6/1.67)F_y = 0.36F_y. These sections are listed in Appendix Table A-4.3 (see Note 3).

Block shear

Where the top flange of a steel beam is coped (so that it may be fastened to the web of a girder while keeping the top surfaces of girder and beam flanges aligned), a mode of failure combining both shear and tension stresses in the beam web must be checked, with the shear and tension failure planes assumed to occur at the surface defined by the bolt centerline, as shown in Figure 4.25.

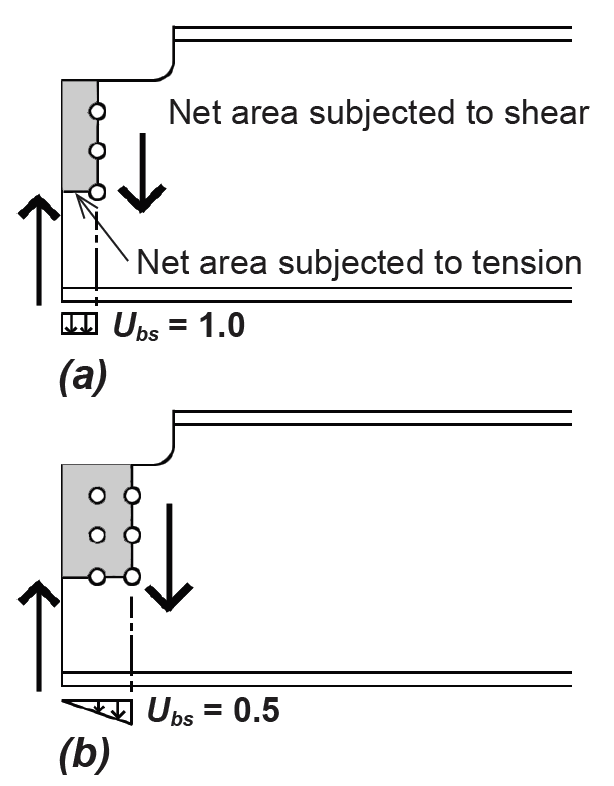
The nominal capacity of such a connection is found by adding the capacity of the net shear area subject to rupture (or the gross shear area subject to yielding) to the capacity of the net tension area subject to rupture. Where both net areas are subject to rupture, the capacity is defined as: R_n = 0.6F_uA_nv + U_bsF_uA_nt. Where yielding governs the failure of the shear area, the capacity is defined as: R_n = 0.6F_y A_gv + U_bsF_uA_nt. The smaller of these two values determines the capacity of the connection for resisting block shear. In these equations, F_u is the minimum tension strength of the material (equal to 58 ksi for A36 steel, and 65 ksi for A992 steel); A_nv and A_nt are the net areas for shear and tension, respectively; A_gv is the gross shear area; and U_bs equals 1.0 for conditions that correspond to uniform tension stress, as in the coped beam with a single line of bolts shown in Figure 4.25a, while U_bs equals 0.5 for conditions that lead to a triangular (nonuniform) tension stress, as in the coped beam with a two lines of bolts shown in Figure 4.25b. The available strength is then found by dividing the nominal capacity by the safety factor, Ω = 2.00.

It is also possible that a mode of shear failure alone, with no tension component, could govern the connection design. In such a case, both yielding on the gross area of the cross section and rupture on the net area need to be checked. For yielding, the nominal capacity, R_n, equals 0.60F_y A_gv, and the available strength, ΩR_n , is determined using a safety factor, Ω = 1.50 (not Ω = 2.00). For rupture on the net area, R_n equals 0.60F_uA_nv, and the available strength, ΩR_n, is determined using a safety factor, Ω = 2.00. All the parameters are as defined above for block shear. The lower safety factor for yielding reflects the relative safety of a yielding mode of failure compared with the more sudden and catastrophic type of failure associated with rupture.

Example 4.5 Find capacity of beam web based on block shear

Problem definition. Find the capacity of a bolted double-angle connection to the web of a coped W18 × 86 wide-flange beam, considering only block shear in the web. Assume A992 steel (F_y = 50 ksi and F_u = 65 ksi) for the beam, and 3/4-in.-diameter bolts. The bolt spacing, s = 3 in., the vertical edge distance, L_ev = 1.5 in., and the horizontal edge distance, L_eh = 1.5 in. as defined in Figure 4.26.

Figure 4.26: Block shear in a coped beam, for Example 4.5

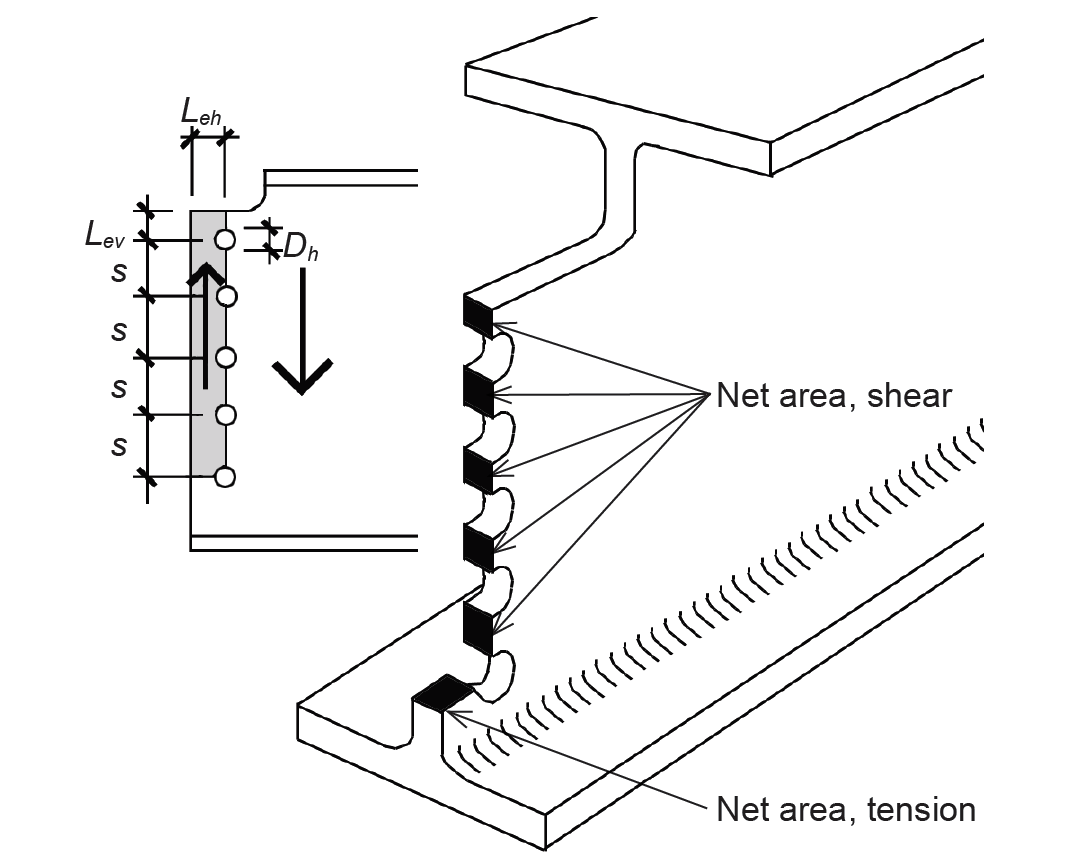
Solution overview. Find the smaller of the capacities based on rupture and yielding of shear area, rupture of tension area, and bolt bearing on the web.

Problem solution

1. Find capacity based on net areas subject to rupture. Lengths along net areas are found by subtracting the lengths of bolt hole diameters from the total (gross) dimension. The net area for shear, A_nv = t_w (4s + L_ev – 4.5D_h) = 0.480(4 × 3 + 1.5 – 4.5 × 0.875) = 4.59 in², where t_w is the web thickness (from Appendix Table A-4.3), s is the bolt spacing of 3 in., L_ev is the vertical edge distance of 1.5 in., and D_h is the bolt hole diameter (found by adding 1/8 in. to the bolt diameter of 3/4 in.). The net area for tension, A_nt = t_w(L_eh – 0.5D_h ) = 0.480(1.5 – 0.5 × 0.875) = 0.51 in², where L_eh is the horizontal edge spacing and D_h is the bolt hole diameter.

The capacity based on rupture of these net areas is defined as: R_n = 0.6F_uA_nv + U_bsF_uA_nt, where U_bs = 1.0 for a single line of bolt holes. Using the material properties defined above, we get: R_n = 0.6(65)(4.59) + (1.0)(65)(0.51) = 212.2 kips.

2. Find capacity based on gross area (yielding) for shear and net area (rupture) for tension. The gross area for shear, A_gv = t_w(4s + L_ev) = 0.480(4 × 3 + 1.5) = 6.48 in², where t_w is the web thickness (from Appendix Table A-4.3); s is the bolt spacing of 3 in., and L_ev is the vertical edge distance of 1.5 in. The net area for tension, as in step 1, is 0.51 in².

The capacity based on yielding of the shear area and rupture of the tension area is defined as: R_n = 0.6F_yA_gv + U_bsF_uA_nt, where U_bs = 1.0 as before. Using the material properties defined above, we get: R_n = 0.6(50)(6.48) + (1.0)(65)(0.51) = 227.6 kips.

3. The governing capacity is the smaller value from steps 1 and 2: R_n = 212.2 kips based on rupture of the net areas.

Deflection

Deflection is based on the same criteria discussed in Chapter 3 for wood beams and involves a comparison of an allowable deflection, typically set at span/240 for total loads and span/360 for live loads on floor beams, to the actual computed deflection. Actual deflections can be computed based on the coefficients in Appendix Table A-4.17 (which are the same coefficients used for wood in Appendix Table A-3.15). Allowable deflection guidelines can be found in Appendix Table A-1.3 (also summarized in Appendix Table A-4.17).

Example 4.6 Design steel beam

Calculator

Problem definition. Using A992 steel, design the typical beam and girder for the library stack area shown in Figure 4.27. Use the generic dead load for steel floor systems. Assume that the beams are continuously braced by the floor deck, and that the girders are braced only by the beams framing into them.

Figure 4.27: Framing plan for Example 4.6

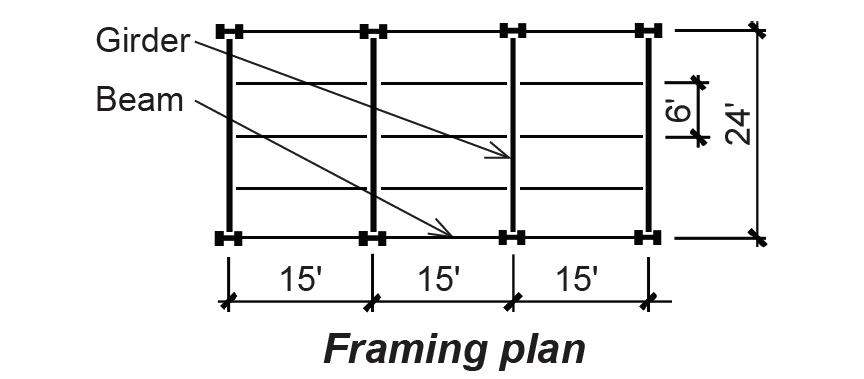
Solution overview. Find loads; compute maximum bending moment and shear force; use appropriate tables to select beams for bending; then check for shear and deflection.

Problem solution

Find loads: From Appendix Table A-2.1, the dead load, D = 47 psf.

From Appendix Table A-2.2, the live load, L = 150 psf.

Beam design

1. Create load, shear and moment diagrams as shown in Figure 4.28 to determine critical (i.e., maximum) shear force and bending moment. The total distributed load, w = (dead + live)(tributary area for 1 linear foot) = (47 + 150)(6) = 1182 lb/ft = 1.18 kips/ft. Live load reduction would not apply even if the "influence" area was not less than 400 ft², because of the library stack occupancy (i.e., the probability of full loading makes live load reduction a dangerous assumption).

Figure 4.28: Load, shear, and moment diagrams for beam in Example 4.6

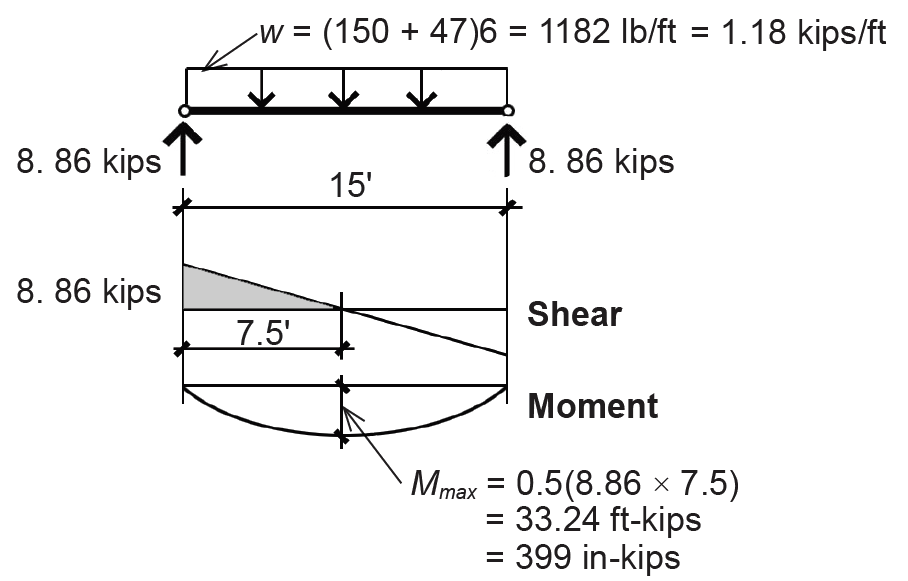
2. Find allowable bending stress: since the beam is laterally braced by the floor deck and the cross section is assumed to be compact, use Equation 4.12 to find Z_req = ΩM_max /F_y = 1.67M_max /F_y. From Appendix Table A-4.1, F_y = 50 ksi for A992 steel, so Z_req = 1.67(399)/50 = 13.33 in³.

3. From Appendix Table A-4.15, select a W12 × 14 with actual Z_x = 17.4 in³ ≥ Z_req. This section is, by definition, OK for bending.

4. Check section for shear: from Appendix Table A-4.3, the actual web area, A_w = d × t_w = 11.9 × 0.20 = 2.38 in².

5. From Equation 4.14, the required A_w = V/F_v = 8.86/(0.36 × 50) = 0.49 in² where, from Appendix Table A-4.2, the allowable shear stress, F_v = 0.36F_y (and not the usual value of F_v = 0.40F_y) because the beam web is unusually slender. Beams requiring such reduced allowable shear stresses are noted in Appendix Table A-4.3. Since the actual web area is greater than the required web area, the beam is OK for shear.

6. From Appendix Table A-1.3 (also summarized in Appendix Table A-4.17), find the allowable total-load deflection for a floor beam: Δ^T_allow = span/240 = 12(15)/240 = 0.75 in. and the allowable live-load deflection for a floor joist: Δ^L_allow = span/360 = 12(15)/360 = 0.5 in.

7. From Appendix Table A-4.17, the actual total load deflection, Δ^T_act = CP(L/12)³/(EI) where:

C = 22.46.

L = 15 × 12 = 180 in. (the term, L, is used for both span and live load).

P = w(L/12) = (150 + 47)(6)(180/12) = 17,730 lb = 17.73 kips.

E = 29,000 ksi (Appendix Table A-4.1, Note 1).

I = 88.6 in⁴ (Appendix Table A-4.3).

Δ^T_act = 22.46(17.73)(180/12)³/(29,000 × 88.6) = 0.523 in.

Since Δ^T_act = 0.523 in. ≤ Δ^T_allow = 0.75 in., the beam is OK for total-load deflection.

8. From Appendix Table A-4.17, the actual live load deflection, Δ^L_act = CP(L/12)³/(EI) where:

C = 22.46.

L = 15 × 12 = 180 in.

P = w(L/12) = (150 × 6)(180/12) = 13500 lb = 13.5 kips (Use live load only!).

E = 29,000 ksi (Appendix Table A-4.1, Note 1).

I = 88.6 in⁴ (Appendix Table A-4.3).

Δ^L_act = 22.46(13.5)(180/12)³/(29,000 × 88.6) = 0.398 in.

Since Δ^L_act = 0.398 in. ≤ Δ^L_allow = 0.5 in., the beam is OK for live-load deflection.

9. Conclusion: The W12 × 14 section is OK for bending, shear and deflection. Therefore it is acceptable.

Girder design

1. Create load, shear and moment diagrams as shown in Figure 4.29 to determine the critical (i.e., maximum) shear force and bending moment. Each concentrated load is twice the typical beam reaction, or 17.73 kips. Alternatively, compute using tributary areas; that is, P = (47 + 150)(15 × 6) = 17,730 lb = 17.73 kips. Live load reduction does not apply even though the "influence" area is greater than 400 ft², because of the library stack occupancy (i.e., the probability of full loading makes live load reduction a dangerous assumption).

Figure 4.29: Load, shear, and moment diagrams for girder in Example 4.6

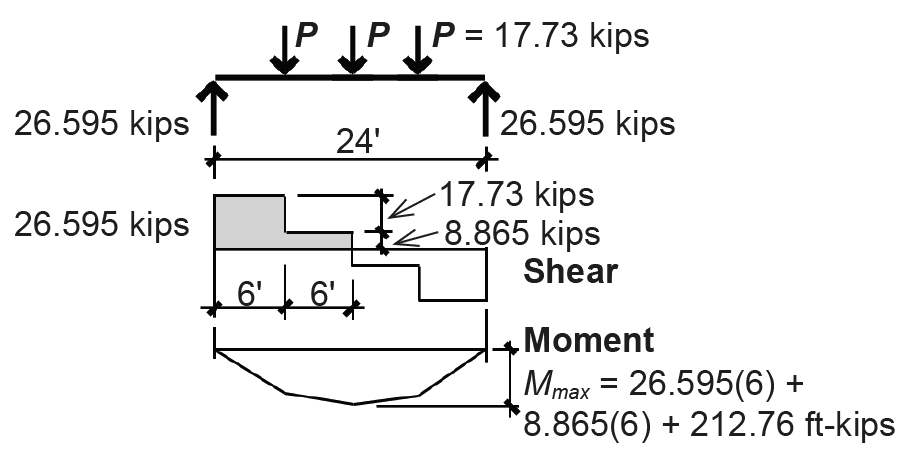
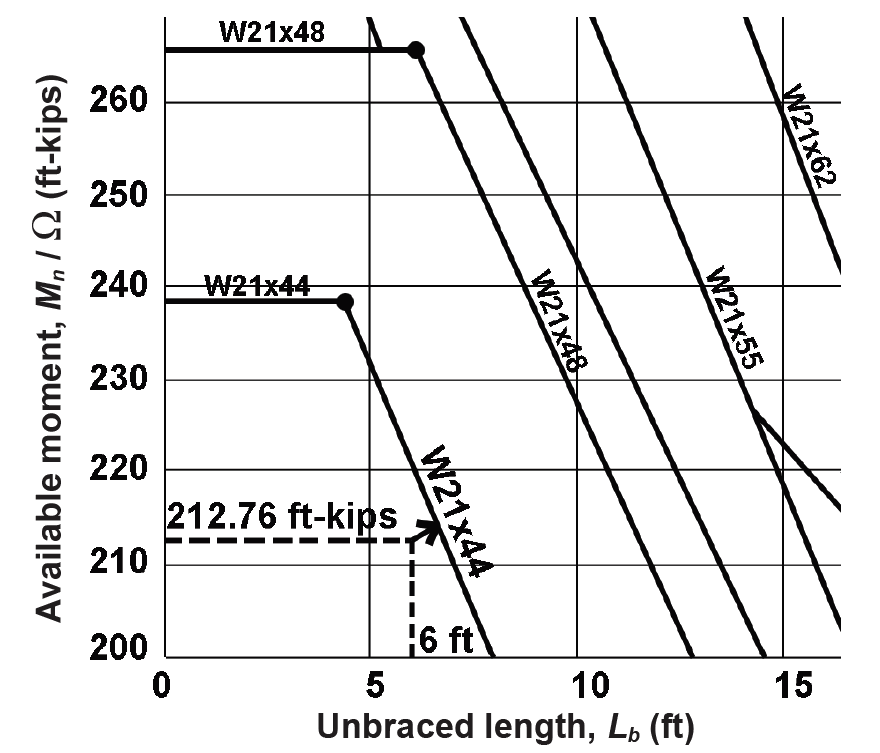
2. Find allowable bending stress: The girder is not continuously braced by the floor deck; rather, it is braced every 6 ft by the beams framing into it, so the unbraced length, L_b = 6 ft. Use Appendix Table A-4.16 to directly find the lightest cross section for bending, based on M_max = 212.76 ft-kips, L_b = 6 ft, and assuming (conservatively) that the "lateral-torsional buckling modifier," C_b = 1.0. Find the intersection of moment and unbraced length (follow the dotted lines shown in Figure 4.30) and then move up or to the right to the first solid line representing the available moment capacity of wide-flange beams. Select a W21 × 44.

Figure 4.30: Selection of W21×x44 beam based on available moment graphs (Appendix Table A-4.16) for Example 4.6

3. Check section for shear: from Appendix Table A-4.3, the actual web area, A_w = d × t_w = 20.7 × 0.35 = 7.25 in².

4. From Equation 4.14, the required A_w = V/F_v = 26.595/(0.40 × 50) = 1.33 in² where, from Appendix Table A-4.2, the allowable shear stress, F_v = 0.40F_y (the usual value of F_v = 0.40F_y applies in this case). Since the actual web area is greater than the required web area, the beam is OK for shear.

5. From Appendix Table A-1.3 (also summarized in Appendix Table A-4.17), find the allowable total-load deflection for a floor beam, Δ^T_allow = span/240 = 12(24)/240 = 1.2 in., and the allowable live-load deflection for a floor joist, Δ^L_allow = span/360 = 12(24)/360 = 0.8 in.

6. From Appendix Table A-4.17, the actual total-load deflection, Δ^T_act = CP(L/12)³/(EI) where:

C = 85.54.

L = 24 × 12 = 288 in.

P = (47 + 150)(15 × 6) = 17,730 lb = 17.73 kips.

E = 29,000 ksi (Appendix Table A-4.1, Note 1).

I = 843 in⁴ (Appendix Table A-4.3).

Δ^T_act = 85.54(17.73)(288/12)³/(29,000 × 843) = 0.86 in.

Since Δ^T_act = 0.86 in. ≤ Δ^T_allow = 1.2 in., beam is OK for total-load deflection.

7. From Appendix Table A-4.17, the actual live-load deflection, Δ^L_act = CP(L/12)³/(EI) where:

C = 85.54.

L = 24 × 12 = 288 in.

P = 150(15 × 6) = 13,500 lb = 13.5 kips (Use live load only!).

E = 29,000 ksi (Appendix Table A-4.1, Note 1).

I = 843 in⁴ (Appendix Table A-4.3).

Δ^L_act = 85.54(13.5)(288/12)³/(29,000 × 843) = 0.65 in.

Since Δ^L_act = 0.65 in. ≤ Δ^L_allow = 0.80 in., beam is OK for live-load deflection.

8. Conclusion: The W21 × 44 section is OK for bending, shear and deflection. Therefore it is acceptable.

« previous section | next section » | contents
unit abbreviations and conversion calculator | references | glossary

© 2020 Jonathan Ochshorn; all rights reserved. This section first posted November 15, 2020; last updated November 15, 2020.