Jonathan Ochshorn
© 2013 Architectural Engineering Department at the Pennsylvania State University, first published as "A Probabilistic Approach to Nonstructural Failure" in the Proceedings of the 2013 Architectural Engineering Conference, State College, Pennsylvania, April 3-5, 2013 (Edited by Chimay J. Anumba and Ail M. Memari, American Society of Civil Engineers—ASCE).
Also see: Designing Building Failures
ABSTRACT
In spite of a virtual epidemic of nonstructural failure (leaking roofs, delaminating finishes, etc.), there is no method for architects to assess the reliability of nonstructural elements within the buildings they design. Structural elements and systems within buildings, on the other hand, are designed so that the probability of failure is acknowledged. The analysis of nonstructural building elements and assemblies is more complex, and raises different issues, than that of structural elements and systems. This paper suggests areas for future research into the probabilistic design of nonstructural building elements by examining the limit states and performance requirements for nonstructural failure (risk assessment); the boundaries of sites within which failure might occur (probabilistic analysis); whether a probabilistic approach to nonstructural failure makes sense; and the consequences of peculiarity and redundancy.
INTRODUCTION
It is commonly acknowledged that nonstructural parts of buildings fail at an alarming rate: roofs leak, flooring delaminates, paint peels, and so on (Chen et al., 2010). If the definition of nonstructural failure is extended to include things like slabs that are not flat, or enclosures that are not energy-efficient, or rooms that function poorly for their intended purpose, or improperly constructed elements that need to be removed and reconstructed, or any number of other criteria for failure, then the rate of failure undoubtedly increases.
Surprisingly, given this virtual epidemic of nonstructural failure, there is no method commonly encountered in practice for architects—even conscientious ones—to assess the reliability of the buildings they design. Of the construction products, systems, and methods that are sanctioned by building codes and available on the marketplace, none provide data from which the reliability of the assemblies into which they are fashioned can be ascertained. Moreover, there are few if any adequate statutory controls based on risk assessment, and there are numerous instances where design entities requiring serious engineering (e.g., building enclosure systems) are left to "the architect who generally specifies, details, and approves" such things, often leading to "significant problems with the faŤades of modern buildings" (Faddy et al., 2003).
If this state of affairs existed for the structure of buildings (structure referring to the columns, walls, beams, and slabs that together resist various forces impinging upon the building), it would be impossible to know whether any given building had an unacceptable risk of collapse. Both life and property would be in danger, and both would be endangered to an extent that was not possible to determine either in the aggregate (e.g., for society as a whole) or in any particular instance (e.g., for the building you are in right now). The analysis of nonstructural building elements and assemblies is more complex, and raises different issues, than that of structural elements and systems. It is the purpose of this paper to examine nonstructural reliability, suggesting areas for future research.
RISK ASSESSMENT
Building elements will fail, and their failure can be understood probabilistically. When journalists and others use phrases that are implicitly probabilistic ("Excess capacity in the economy may well dampen cost and price pressures for a period…"), it is easy to conclude that they are simply hedging their bets. By stating that excess capacity may well dampen price pressures, one can conclude with equal certainty that excess capacity may well not dampen price pressures. In other words, something may happen, or it may not happen. We are left with nothing but the appearance of wisdom.
Yet probabilities can be useful, even when they correspond not to a classic, well-defined random occurrence (e.g., rolling dice or flipping coins), but to subjective, expert opinion (e.g., there will be a 30% chance of rain tomorrow). Such expert opinion, especially when encountered in building science, may be based purely on a kind of epidemiological or actuarial approach—where the historic incidence of a particular outcome is used to extrapolate about the probability of future occurrences—or may draw on both historic rates of occurrence as well as underlying causal hypotheses.
In the case of structural failure, building codes make assumptions based on evidence assembled from laboratory tests and from the performance-history of large groups of structures, without having any specific knowledge about the likelihood of failure for any particular proposed building. However, by tracking the number of structural failures over time, code agencies (and politicians who turn model codes into legal rules and regulations) can make judgments about the efficacy of legislation and can rationally modify such legislation when new information is generated, typically in the wake of disasters like earthquakes, hurricanes, or even man-made attacks. Yet such strategies are rarely employed for nonstructural building elements.
Limit states
MacGregor (1976) discusses the concept of limit states to define various criteria for which structures must be designed. In "limit states design the designer is expected to identify all the critical limit states and consider them either explicitly by design checks or implicitly by satisfying certain detailing requirements or minimum reinforcement requirements. Ideally, the limit states would be expressed in terms of performance requirements which are essentially independent of the structural material."
Structural design is not limited by a single mode of failure; rather, there are several criteria (limits) that must be checked, including yielding or rupture (whether due to tension, compression, or shear) and deflection or deformation. Still, the types of limits are fairly well-defined; variations in material and geometric properties are, for the most part, regulated and tabulated within state-sponsored building codes based on the work of consensus-driven institutes and associations; and techniques have been developed to analyze and design structures so that they remain within their limit states. In contrast to the relative simplicity of structural limits, analogous limit states for nonstructural failure are far more diverse, and techniques to analyze and design for such limit states are much harder to find. Such nonstructural limits include things like water intrusion, air intrusion, vapor-condensation, heat loss, bowing, cracking, peeling, as well as any number of serviceability-type issues: noise, vibration, glare, and so on. Not only are nonstructural limit states more diverse, but the number of different materials and potentially damaging material interactions—especially when exposed to diverse environmental conditions—is far greater for nonstructural, than for structural, building elements.
Given the multiplicity of both limit states and material/environmental interactions, the question remains whether it is possible, or feasible, to establish the equivalent of "design strengths" (i.e., limiting values based on specified levels of risk) for nonstructural construction elements, and to develop corresponding design methods. Aside from the enormous task of identifying and documenting failure probabilities for all material interactions and all known limit states, additional difficulties would need to be overcome, including the following:
Product specifications may refer exclusively to particular proprietary or nonproprietary systems, in spite of the fact that such systems may not be entirely self-sufficient. In other words, a system may need to connect to other systems at its boundary, and the entire range of possible boundary conditions may not be specified or tested.
Systems may be used or configured in ways that differ from what has been tested and approved by manufacturers (much like the use of "off-label" drugs in medicine).
All possible modes of failure, and all possible combinations of these failure modes, are not always addressed within system specifications.
Idealized, specified conditions (including the required cleanliness of material surfaces, the prevailing temperature and humidity during installation, the required coverage of adhesives or heat welding, and so on) may not be met; and, equally important, there may be no systematic means either to certify compliance or to test, after the fact, whether the installed product satisfies the specifications.
Probabilistic analysis
In order to be more precise about the risk of failure, it is useful to define the boundaries of sites within which failure might occur. Depending upon the type of failure, such sites might be dimensionless quantities (e.g., number of penetrations in an air barrier) or else the familiar dimensional measures for various geometric objects (e.g., length of seams in an EPDM roof; area of paint on a flat surface; or volume of contaminated air in a room). A particular quantity could then be chosen to define the nominal magnitude for each site (e.g., 1 m.; 100 ft2; 50 gal.) so that it can be systematically evaluated and compared, and so that rational standards for reliability can be developed. Methods for determining system reliability, while well-established, are quite complex and beyond the scope of this paper. For an overview of reliability computation methods and strategies, see Blischke and Murthy (2003).
Site, events, and event density
If we call every potential site of nonstructural failure, along with its mode or modes of failure, an event, it is useful to distinguish between negative outcomes that are independent of the number of events, and negative outcomes whose likelihood of occurrence increases with the number of events. In the first case, a particular event (e.g., the bringing together of incompatible materials, or the use of an item with insufficient strength or durability) will result in failure, whether it occurs only once or numerous times. The mechanism of failure guarantees a negative outcome. Yet even with this certainty of failure, the overarching probabilistic framework for understanding failure remains valid: whether the causes of failure were due to errors in the drawings and specifications created by the architects and design consultants, or by errors in fabrication or installation, or by any other action, it is often only in retrospect that one can say that a particular event was certain to cause failure. Without this knowledge, all one can say is that a building might fail, or has a probability of experiencing failure. This type of failure is independent of "scale" or complexity—a greater number of similar events does not increase the chance of failure, but only increases the number of failure events.

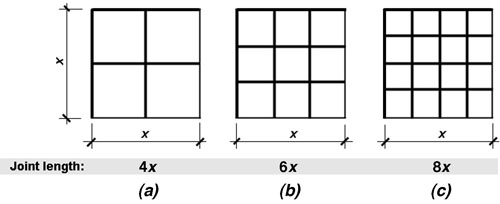
Figure 1. Abstract representation of variable joint length
In the second case, a particular building element may not be intrinsically predisposed to fail, but rather may have a chance of failure based on the combined influence of any number of variables. Depending on the mechanisms or modes of failure that correspond to these variable conditions, the probability of failure can be determined in relation to the number of times that such events occur, that is, in terms of the event density. For example, in the case of a sealant joint between two panels whose integrity over time depends only on a single variable (let's say that this variable is the proper installation of a backing rod with integral bond breaker), and if the variable is well-defined and random (that is, if there is an equal likelihood that the backing rod at any site—e.g., along any given linear foot of the joint—will be properly installed), then the probability of failure is proportional to the total number of sites, i.e., to the total length of joints.
For the joints abstractly represented in Figure 1 (shown with bold lines), a given panel size is subdivided in three different ways (cases a, b, and c) such that the total joint lengths are 4x, 6x, and 8x respectively. The probability of failure is therefore one and a half times as great in case b as in case a, and two times as great in case c as in case a.
Multiple failure modes
On the other hand, there may be more than one variable in play, each of which has some likelihood of causing joint failure independent of the other. Because so many different modes and manifestations of architectural failure—condensation, leaks, cracks, corrosion, deterioration, mold, etc.—are potentially present at every building failure "site," and because these possible modes of building failure are often not mutually exclusive, the probability of failure does not increase proportionally, but rather geometrically or even exponentially, when multiple modes of failure are considered.
For example, the integrity of the joints in Figure 1 may be threatened not only by improper installation of a backing rod with integral bond breaker, but by the cleanliness of the panel surfaces to which the sealant is directly adhered. If it is assumed that the probabilities of each separate outcome are the same and not mutually exclusive, then the chance that a given length of joint will fail by either of the failure mechanisms is double the probability that the joint will fail if only one of the failure mechanisms is in play. In other words, the probability of failure is four times as great in case c, with both failure mechanisms in play, as in case a, with only one failure mechanism in play.
Assuming that each failure mode has the same probability of experiencing a failure event, the overall probability of failure increases exponentially as both the number of non-mutually-exclusive failure modes and the building's complexity or event density (in this case modeled as a simple increase in the length of joints) increase linearly. That is:
where
P(Fc) = the overall probability of experiencing a failure event (with constant probabilities of failure)
no = the number of occurrences (event density)
nm = number of independent failure modes
p = the probability of experiencing a failure event for any one mode of failure for a single occurrence (event density = 1)
A building with a single failure mode and an event density of 1 has a probability, p, of experiencing a failure event; doubling both the number of failure modes and the event density results in an increase in the probability of experiencing failure events to 4p; tripling both the number of failure modes and the event density results in a probability of 9p; and quadrupling both the number of failure modes and the event density results in a probability of 16p. This pattern can be clearly seen in Table 1.
Table 1. Probability of failure events in relation to event density and failure modes*
| Number of failure modes | Assumed probability of failure event | Relative number of occurrences (event density) | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | for mode 1 = p | p | 2p | 3p | 4p |
| 2 | for mode 2 = p | 2p | 4p | 6p | 8p |
| 3 | for mode 3 = p | 3p | 6p | 9p | 12p |
| 4 | for mode 4 = p | 4p | 8p | 12p | 16p |
* Assuming each failure mode has an equal probability of failure within an occurrence space.
While these results assume that each mode of failure within a given occurrence space has an equal likelihood of producing a failure event, similar conclusions can be drawn from a more general formulation of the problem in which probabilities of failure for each failure mode within an occurrence space may vary. In that case, we get:
where P(Fv) is the overall probability of experiencing a failure event (with variable probabilities of failure), the other parameters as defined for Equation 1 [and where ∑ is the sum from n = 1 to n = nm].
The combination of multiple failure modes along with increasing building complexity (event density) results in an increasing probability of failure. Where multiple failure modes are found to occur together at a site, it might be possible to group them as a single event whose probability of failure equals that of the various individual failure mode probabilities combined. However, there are several types of failure mode interactions where such an assumption does not apply:
1. In some cases where two or more modes combine, the failure probability increases beyond what would ordinarily be expected. For example, hurricane conditions with wind driven rain (mode 1) and wind-borne debris (mode 2) each carry an independent potential for damage. However, debris that breaks glass in the context of wind-driven rain will carry more risk of failure than what would be calculated for each mode of failure considered separately (i.e., with the two probabilities of failure simply "added" together).
2. In some cases where two or more modes combine, a failure probability comes into play where none previously existed—that is, where no failure modes per se existed until they combined to create a new failure mode. An example would be two metals that are in contact ("mode" 1) along with an electrolyte such as water that is present on the surface ("mode" 2). Two innocent practices (neither of which is a problem considered in isolation), when combined, create a new failure mode (galvanic corrosion).
3. In some cases where two or more modes combine, the failure probability actually decreases compared to the two modes acting separately. For example, deploying redundant layers, each of which when considered separately has a probability of failure proportional to some measure of quantity (e.g., length, or area), may actually result in a lower probability of failure. Storm windows and double sealant joints create a greater quantity of joints with the potential to fail, yet result in a decreased probability of failure. In such cases employing redundancy, the overall risk of failure is no longer necessarily defined by the addition of the separate probabilities. As an extreme example, consider a roof membrane where manufacturing defects (holes) have a 0.1 probability of occurring within a given unit area. If two such units of area are deployed side by side, the overall chance of failure doubles from 0.1 to 0.2. But if the two membranes are placed one over the other, so that failure only occurs when holes in each membrane align, the chance of having two such holes (one per membrane) within the same unit of area decreases to 0.01, and the chance of such holes actually aligning (the precondition for failure) is even smaller.
DOES A PROBABILISTIC APPROACH MAKE SENSE?
It is apparent that not only are nonstructural failures costly and inconvenient for building owners and users, but that the risk of such failure is difficult or impossible to determine by those responsible for the design of buildings. Does it follow that the "status quo" method of not considering the probability of nonstructural failure should be replaced with a probability-based method? Whether or not a risk-based approach results in lower, or at least more predictable, life-cycle costs, a number of potentially countervailing issues must be considered.
Legal/constitutional/political issues
Structural design methods incorporating a probabilistic strategy to control failure are not only promulgated by not-for-profit code councils and industry-sponsored institutes (ICC, AISC, AITC, ACI, etc.), but are also adopted by governmental entities in the form of building codes, thereby becoming legally binding and enforced by state power. On the other hand, property owners and builders—supported by the political and legal infrastructure—have sometimes been able to successfully block both structural and nonstructural initiatives that would increase safety but also increase costs. In the case of nonstructural initiatives that might not only increase costs, but also restrict design choices, courts may well strike down provisions constraining the freedom of architects, manufacturers, and property owners in cases where a countervailing "health, safety, and welfare" societal benefit is not sufficiently evident.
Cost-benefit issues
MacGregor (1976, Fig.19) breaks down the cost of building structures into three components: "production," "maintenance," and "insurance." When production and maintenance costs decrease beyond a certain point (corresponding to increasingly dangerous building structures), insurance costs increase dramatically, presumably reflecting the increasingly untenable risks that arise when the costs of providing adequate structural safety are not met. Thus, the added costs brought about by governmental intervention to promote structural safety have the benefit of reducing costs associated with loss of life and property; and the benefit is arguably greater than the cost. Whether the same sort of calculation can be made for nonstructural building elements is less clear. Among the significant costs of structural collapse are loss of life, and loss of the building's ability to function, neither of which is intrinsic to nonstructural failure (Faddy et al., 2003, p. 113). It is possible that it is cheaper to repair failed nonstructural building elements as these failures become manifest, than to anticipate all possible failure modes in advance and to design and construct buildings with a predetermined risk of failure.
Problems with obtaining data
Manufacturers are not required, and are not generally interested, in publishing data about the reliability of their products, even if there were standards for how to do this. For one thing, competition with other manufacturers, and the absence of mandatory disclosure based on established protocols, favors hyperbole over accuracy. In addition, manufacturers are often unwilling to evaluate or describe the behavior of their products in relation to adjacent or connecting products over which they have no control.
CONCLUSIONS
The probabilistic nature of building failure is well understood in structural engineering, where factors of safety are explicitly calibrated in such a way that structures fail at a desired rate. It is understood that avoiding all structural failure is not possible; the intention is therefore to reduce (or increase) the probability of failure to a politically/economically acceptable rate. Refinements in structural design methods have made the risk of failure more uniform—less subject to differences in materials or types of loads. Whereas the probability of structural failure (i.e., the actual collapse of buildings or structural components like beams or columns) is made explicit within the design methods enforced by building codes and, in fact, forms the very basis of structural design, the design of nonstructural parts of buildings has no underlying probabilistic basis. That is, when architects create drawings and specifications for buildings, they have no basis for determining the probability of nonstructural failure. A probabilistic basis for such failure is acknowledged neither in theory nor in practice. Nevertheless, it is still possible to draw some important conclusions about the nature of such failure, and point towards future areas of research.
Peculiarity and complexity
Perhaps the most important conclusion derives from the fact that, for unusual (peculiar or complex) architectural designs, the interaction of materials, systems, geometries, environmental conditions, installation methods, and so on, is rarely systematically tested or theoretically grasped. Conventional construction details and methods, on the other hand, have at least a track record of generally successful (or unsuccessful) application. While the lack of a consistent measure of reliability applies to such conventional systems as well, there is at least an informal understanding of how such systems perform over time. For this reason alone, one can state that nonstructural failure will generally increase as the peculiarity or complexity of the architecture (i.e., the deviation of its design from well-established norms) increases.
This conclusion requires a disclaimer: it presupposes an ordinary level of attention given to all aspects of building design and construction. In other words, it is assumed that little or no original research is undertaken to establish the behavior of unusual design elements or their interactions. The nonstructural failure of the John Hancock Tower in Boston may serve as an example of a building designed with unconventional curtain wall details, but without adequate testing and research (Campbell, 1988). Of course, if one has the budget, the time, and the expertise, it is certainly possible to reduce the probability of failure when designing unusual or complex buildings. An example of such an attempt can be seen in the glass enclosure system developed for La Cité des Sciences et de l'Industrie in Paris as described by Rice (1995).
Redundancy
The benefit of redundancy, examined from a probabilistic standpoint, is a relatively unexplored and potentially fruitful area of research. In the hypothetical and schematic example cited earlier, providing two roof membranes instead of one doesn't merely cut the risk of failure in half, but rather decreases the risk of failure by an order of magnitude. Of course, it is crucial that any strategy employing redundancy take into account the specific mode of failure: adding an extra (redundant) layer of paint over an improperly prepared substrate confers no particular advantage since the utility of the redundant layer depends on the integrity of the layer below. In other words, the conditional probability of failure of the redundant layer, given failure of the layer below (and therefore failure of the system as a whole), is 1.0, conferring no advantage. At the other extreme, the conditional probability of system failure for the two membranes discussed earlier, each membrane having a failure probability of 0.1, is 0.1 × 0.1 = 0.01, a significant improvement.
Conventional practices, such as the provision of roof overhangs, can be reevaluated in this light. For a given exterior wall surface area, if the probability of failure due to water intrusion through an unintended hole in the wall is, say, 0.05, and if the probability that wind-driven rain will reach that wall surface is 0.07 when an overhang is in place, then the conditional probability of failure with an overhang is 0.05 × 0.07 = 0.0035, a dramatic reduction in risk compared with the hypothetical failure probability of 0.05 without the overhang.
Limitations of traditional architectural drawings and specifications
Architectural drawings do not attempt to represent each nonstructural element and its conditions; rather, general descriptions and notes apply to large conglomerations of elements, under the assumption that all the various conditions actually encountered, but not specified, will be somehow dealt with in the field. To the extent that this practice is not remedied through comprehensive and carefully checked shop drawings, it constitutes a major deficiency in the process of architectural construction.
Typical building specifications do not supply consistent, and useful, instructions for building contractors. Instead, advice like this is common: "…it is essential to ensure the substrate is structurally sound, clean, and dry. Prior to the installation, the surface should be protected and free of any potential substance or debris that might reduce or prevent adhesion" (Miller, 2011). Unfortunately, nothing in such specifications provides a method, a protocol, or a test to ensure that the desired conditions are met. It is as if such paragraphs were written by lawyers, hoping to establish a basis for successful litigation in the event of building failure, rather than by architects and engineers seeking to actually create conditions that will reduce and control the probability of failure. Yet even conventional tests are problematic, as they are not designed to provide data from which the risk of failure can be determined. Any curtain wall assembly can be mocked up and tested per ASTM guidelines, but it is not feasible to construct 500 such mock-ups in order to get a sense of the actual risk of failure.
Performance based criteria, especially those that cannot be explicitly measured ("ensure that the substrate is structurally sound") rely on the conscientiousness and expertise of architects and builders who most often lack the tools, and in many cases may prefer not to jeopardize their firms' profitability by expending discretionary resources, to determine the failure risk of the assemblies they design and build. What seems clear is that prescriptive mandates—designed so that builders and architects use assemblies, systems, or products engineered according to explicit probabilistic criteria for failure—are most likely to reduce the current epidemic of nonstructural building failure.
REFERENCES
Blischke, W. and Murthy, D. (2003) "Introduction and Overview," Case Studies in Reliability and Maintenance, Blischke and Murthy (Eds.), John Wiley and Sons, Inc.
Campbell, Robert (1988) "Learning from The Hancock," Architecture, March 1988, pp. 68-75.
Chen, S., et. al, Eds. (2010) Forensic Engineering 2009: Pathology of the Built Environment, American Society of Civil Engineers, Reston, VA.
Faddy, M., Wilson, R., and Winter, G. (2003) "The Determination of the Design Strength of Granite Used as External Cladding for Buildings," Case Studies in Reliability and Maintenance, Blischke and Murthy (Eds.), John Wiley and Sons, Inc.
MacGregor, J. (1976) "Safety and limit states design for reinforced concrete," Canadian Journal of Civil Engineering, Vol. 3, No. 4, Dec. 1976, pp. 484-513.
Miller, D. (2011) "Alternate Methods for Installing Engineered Stone," The Construction Specifier, Jan. 2011, Vol. 64, No. 1, pp. 26-31.
Rice, P. and Dutton, H. (1995) Structural Glass, E & FN Spon, London, New York.
First posted 19 April, 2013; last updated 19 April, 2013