Teaching Technology: What Do Architects Need to Know About Structures?

COMMUNICATING WITH CONSULTANTS. The second rationale for teaching structures is that, given the extent to which the engineering profession has taken over the task of actually designing structures for buildings, architects must at least be able to discuss structural design issues with these engineers. For one thing, the architect is more often than not the leader of the design team; it would be difficult to exercise this leadership role, involving the coordination of all the design and engineering specialties, without possessing some knowledge about each area. Equally important, it would not be possible to successfully collaborate with engineers on large scale projects.

Sullivan's Guaranty Building, Buffalo, NY with ambiguous expression of column grid

On the other hand, it is important not to overstate the case. For once a structural system has become commonplace, it can be successfully integrated into an architectural design without much consideration for structural theory or behavior, at least on the part of the architect. Consider, for example, the steel skeleton frame, to which so much attention was given in the first half of this century as a determinant and generator of architectural form. In many cases, the architect's qualitative understanding of structural theory with respect to this type has been largely reduced to the deployment of columns along grid lines.

LITERACY VS. COMPETENCE

Given the "division of labor" within the profession of architecture (and therefore within the schools) in which practitioners with various levels and types of technical competence find useful employment, it is improbable that a single unified purpose will emerge, or that a single strategy for teaching structures to architects will be found or should be sought. What is important is not that a particular selection of structural topics and methods be canonized, but rather that course objectives be articulated within each school, and course content be made to correspond to those objectives in a more systematic way.

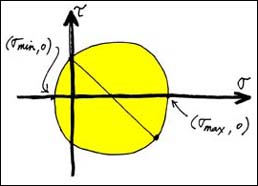
Each diameter of Mohr's Circle shows an equivalent state of bending and shear stress.

In all of the examples cited, considerable effort is expended to derive the rather complicated relationships between principal stresses, on the one hand, and the conventional bending, axial and shear stresses with which we are more familiar. Additionally, the graphical representation of this relationship invented by Otto Mohr is usually presented. Yet in none of the examples is a numerical method suggested that would actually allow one to solve the types of problems for which the topic was presumably introduced in the first place. Thus the insight into, and manipulation of, states of stress encouraged by the use of this topic tends to become rather petrified and obscure; the complexity of the whole procedure seems out of proportion to its actual application in the design or analysis of the types of simple structural elements to which architects are primarily exposed.

In spite of this, I am not suggesting that this particular topic necessarily should be omitted. For as we have seen, there may be reasons for introducing topics other than just solving structural problems. For example, the ribbed slab used by Nervi in the Gatti Wool Factory in Rome (1951-53) becomes inexplicable without some understanding of principal stresses, as does the pattern of web-shear cracking in a reinforced concrete beam and the rationale for using inclined longitudinal or shear reinforcement. The real issue becomes clearer when we assess the importance of the topic according to the dual criteria of literacy and competence.

From the point of view of structural competence, it would be necessary not only to master the technique, in this case of determining the magnitude and direction of principal stresses resulting from all possible combinations of axial, bending and shear-type stresses, but more importantly to be able to use the technique in a purposeful way. Given the tendency of structural design codes to propound design and analysis methods for typical structural elements in which these principal stresses are not explicitly acknowledged — in other words, where a purposeful application of those techniques is made largely irrelevant by the standardized procedures suggested by design manuals — it is doubtful whether competence, defined in this way, is a reasonable goal in an architectural curriculum.

From the point of view of structural literacy, on the other hand, what becomes crucial is not so much the technique itself, but that connections be made between the derivation or presentation of rather abstract sets of relationships — the formula for the maximum principal stress has no obvious intuitive meaning, except perhaps in the graphic form invented by Mohr — and the whole range of results to which they contribute. In the example just cited, these results might well include all of the issues we mentioned: the failure mechanism of beams; the crowding of isostatic lines at points of stress concentration; the complex combinations of stress in thin shell structures. Where the results are found to be either inconsequential, obscure, or in some way beyond the scope of the architectural curriculum, then the topic itself might well be omitted. Where the results are deemed important, then the derivation or manipulation of mathematical formulas ought to be considered, not as an end in itself, but rather judged by the extent to which it contributes to a deeper appreciation of those results.

STRUCTURAL DUALITIES

This conflict between literacy and competence in the teaching of structures to architects could be framed as a series of dualities in which the second term is typically suppressed. In the previous example, the treatment of axial, bending and shear stress as a collection of discrete entities, each with its own method of analysis and its own criteria for design, was contrasted with the more unified notion of an elemental "state of stress" in which the combined action of shear, bending and so on was seen to produce inclined stresses of greater magnitude than those computed separately.

In a similar way, a whole series of such pairs — statics vs. dynamics; member vs. system; strength vs. stiffness; elastic vs. inelastic; even abstraction (load, shear, moment diagrams) vs. reality (actual structure/building behavior) — all can be seen as expressing a certain tension between the desire for competence and the search for structural literacy. This tension comes about because, by essentially circumscribing the areas of inquiry to those topics represented by the first terms and thereby providing a semblance of structural competence, the kind of structural literacy that would be engendered by an appreciation of both terms of the pairs tends to suffer. Consider the following example.

Yet these arguments are really an explanation of why learning about determinate structures might be useful; not an explanation of why indeterminate analysis need not also be taught to architects. Perhaps the explanation is too self-evident to be stated explicitly: while a qualitative understanding of the behavior of all types of structures (including indeterminate ones) is certainly important, the mathematical knowledge prerequisite to an understanding of modern indeterminate analysis techniques cannot reasonably be required of architectural students.

As a result, a number of approaches have been used, alone or in various combinations, to introduce this subject to architectural students: non-mathematical examinations of indeterminate structures based on intuition, models, etc.; approximate analyses (based on simplifying assumptions about relative stiffness or location of inflection points) that reduce the problems to statically determinate ones; iterative methods, such as moment distribution, in which "exact" solutions are approached using relatively simple mathematics; and finally, the presentation of results without explanation, as occurs, for example, in the "beam diagrams and formulas" of the AISC Manual of Steel Construction, or in the analysis of indeterminate structures using computers. In the latter case, results can be obtained without having any knowledge of the matrix algebra underlying the method.

PEDAGOGICAL GOALS

The appreciation of structures that can be attained through both qualitative and quantitative study within the limited framework normally provided by architectural curricula should not be confused with the type of creative act outlined by Candela. Even the most rigorous presentation of structural concepts will not promote real structural competence if the material is not internalized — taken apart and re-synthesized — by each student over a period of many years of careful study. And where sufficient information about the structural systems used in the overwhelming majority of building types can be assimilated by the typical architect without such a lifelong commitment to the pursuit of structural knowledge, it is unrealistic to expect such an effort to be made. What should be expected is a certain degree of structural literacy, in which mathematical relationships are studied and employed, not to engender a false sense of competence, but so that the vocabulary of structures, intrinsic to any definition of literacy, becomes more tangible and intelligible.

NOTES